#数楽 グレブナー基底入門 (論理パズルを解く話を題材に)https://twitter.com/fronori/status/765693630623289344 …https://twitter.com/syura1357/status/765556323970711552 …→ https://kakuyomu.jp/works/1177354054880542193 …続きのツイートでをWolframAlphaの使用例を示します。
#数楽 x^2-2=0, y^2-3=0, z-x-y=0 を解く→ http://www.wolframalpha.com/input/?i=Groebner basis of {x**2 - 2, y**2 - 3, z - x - y} …非線形の場合も含めてこの手の連立代数方程式を「解く」ための一般論があるという話。cf.https://kakuyomu.jp/works/1177354054880542193/episodes/1177354054880647628 …
#数楽 中学生くらいになったらWolframAlphaを使った方がいいと思う。連立方程式も解いてくれるし。iPhoneでもAndroidでも有料のWolframAlphaアプリを入れるとCPUの使用時間の制限が外れて便利。保護者は子供にこのアプリを買ってあげるべき。
#数楽 https://www.slideshare.net/mobile/konn/grbner …技術者が知るべきグレブナー基底石井大海いまやグレブナー基底くらいは「常識」だよね。受験数学を教えている人達の中にも知っている人達は結構いるんじゃないかな?
#数楽 http://konn-san.com/math/groebner-and-entrance-math.html …今年の冬は Gröbner 基底でスーパー大学受験ガール!1. 今年の受験は Gröbner 基底で乗り切れ!こういうノリの話は当然出て来るよね。
#数楽 グレブナー基底の計算によって、x+yをx^2+y^2とx^3+y^3で表わす公式を求める→ http://www.wolframalpha.com/input/?i=GroebnerBasis[{x+y-a,x**2+y**2-b,x**3-y**3-c},{a,x,y,z,b,c}] …アプリ経由でCPU使用時間の制限を外す必要があるかも。子供の保護者はWolframAlphaのアプリを買ってあげるべき。
私がよく宣伝しているWolframAlphaでグラフを描いてみました。(n=600, p=1/6 の二項分布)http://www.wolframalpha.com/input/?i=plot+y=binom(600,x)(1/6)**x(5/6)**(600-x),+0
n=600, p=1/6の二項分布でのぴったり100の確率をWolframAlphaで計算してみました。http://www.wolframalpha.com/input/?i=binom(600,x)(1.0/6)**x(5.0/6)**(600-x),+x=100 …P(X=100)=0.0436643
n=6000, p=1/6の二項分布で990から1010になる確率の直接的計算http://www.wolframalpha.com/input/?i=sum_%7Bk=990}^{1010}+binom(6000,k)(1.0/6)**k(5.0/6)**(6000-k …).
一つ前の奴は最後の)が欠けてしまいましたが、WolframAlphaが補って計算してくれました。WolframAlphaはテキトーに数式を入力すれば結構適切に解釈して計算してくれます。
統計学では二項分布などについては「中心極限定理を使って正規分布で近似して標準正規分布の数表を使って近似値を出す」というのが「伝統的な話」になっています。
n=6000, p=1/6 の二項分布と平均np=1000, 分散np(1-p)の正規分布のグラフの同時プロットhttp://www.wolframalpha.com/input/?i=plot+y=binom(6000,k)(1./6)^k(5/6)^(6000-k),+y=e^{-(k-6000(1/6))^2/(6000(1/6)(5/6)2)}/sqrt(2π6000(1/6)(5/6)),+900
「サイコロを6000回ふることをワンセットにして、6000回ふることを何度も繰り返したとき、6000回中に1の目が出る回数はどのように変動するだろうか?」のように考えることができれば理解が一歩進むと思う。経験分布も確率変数であることの理解には慣れが必要かも。
#数楽 nはそこそこ大きいとする(n≧30くらいとする)。サイコロをn回ふる行為をたくさん繰り返すとき、n回中1の目が出る回数はどのように分布するだろうか?たくさん繰り返せばn/6をピークとする釣鐘型の分布が得られます。続く
#数楽 続き。分布のばらつきの幅を表す指標である標準偏差はσ=√(n(1/6)(5/6))であり、n/6を中心に左右に2σの範囲に95%程度が分布するだろうと予想することができます。
#数楽 たとえばn=6000回サイコロを振ると1の目が出る回数が1000±58の範囲に入る確率は95%程度になります(どんぶり勘定)。こういうどんぶり勘定の背景には「正規分布で近似できる」という中心極限定理があります。続く
#数楽 それでは、1から6の目まで各々の目が出る回数を考えたらどうなるでしょうか?多次元的正規分布にあまり触れていない初歩的な統計学の教科書ではいきなりピアソンのカイ二乗統計量を持ち出して、「n→∞でカイ二乗分布に従う」と書いてあるかもしれません。続く
#数楽 続き。個人的にそういう天下り的な理解をするのではなく、二項分布の正規分布による近似(分布がある特定の釣鐘型になる話)をすなおに拡張して、多項分布を多次元正規分布による近似を理解したい所だと思います。続く
#数楽 続き。サイコロの場合にはn回中iの目が出る回数をk_iとすると、n回サイコロをふる行為を繰り返したときの6次元空間中の(k_1,…,k_6)の分布は、(n/6,…,n/6)をピークとする平べったい釣鐘型になります。続く
#数楽 続き。分布が平べったくなるのは、1から6目が出る回数の総和はnになるので、条件k_1+…+k_6=nで定義される6次元空間中の5次元超平面に分布が制限されるからです。その分布のグラフを描くためには横軸5次元縦軸1次元の6次元が必要になる。
#数楽 1から3の目が等確率で出るルーレットをn回まわして1の目が出る回数をk、2の目が出る回数をlとすると、((k-n/3)/√n,(l-n/3)/√n)の分布はnが大きなとき分散1/3-(1/3)^2、共分散-(1/3)^2の正規分布で近似できます。続く
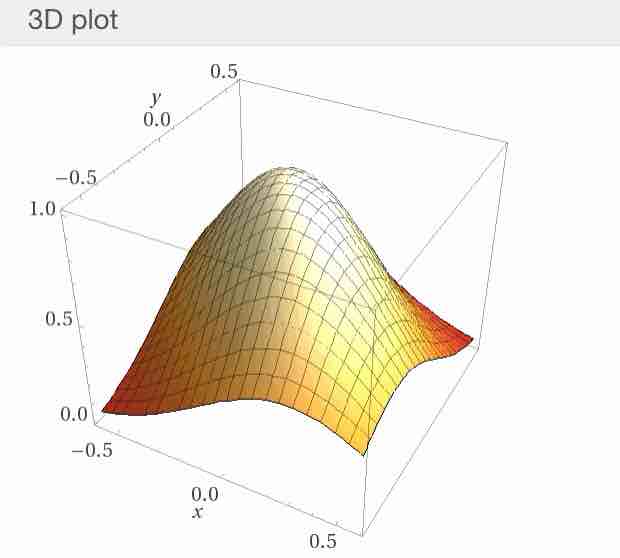
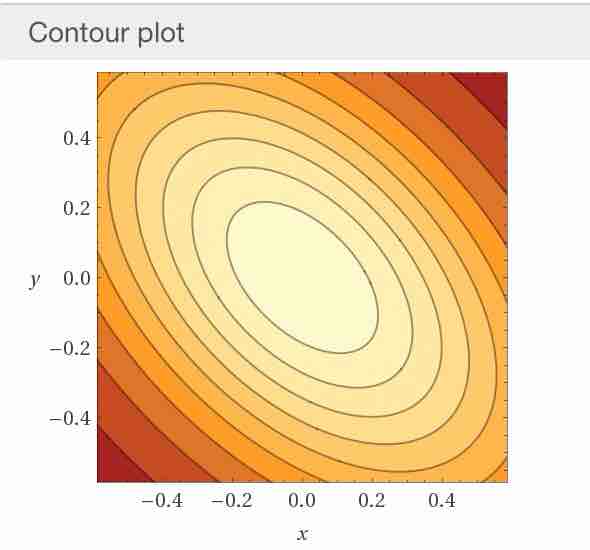
#数楽 等高線は添付画像の通り。これらのグラフを見れば、それらが「二項分布を山型(釣鐘型)の分布で近似できる」という話がどのように3つ以上の目が出る場合(多項分布)の場合に拡張されるかがなんとなくわかると思う。pic.twitter.com/BLSBB2HQuV
#数楽 「二項分布は正規分布で近似し、多項分布の場合にはピアソンのカイ二乗検定を使う」という理解は実用的には便利ですが、「二項分布も多項分布もどちらも同じように考えることができる」というようにも理解しておきたいものだと思います。
1~3の目だけでて、それぞれの確率がp,q,r(p+q+r=1)の場合、3項分布の極限としての3項分布は、Aexp{ー(x^2/p+y^2/q+z^2/r)/2}(x+y+z=0)でいいのでしょうか?
訂正 3項分布の極限としての正規分布はAはサボって計算していないけど、x+y+z=0に注意して全範囲で積分して1になるように調整する。3項分布を√nで補正して、微分方程式を作って解いたのですが。
そうはならないです。exp()の中にxyのような項も入って来ます。あと部分空間への「制限」は「デルタ函数」をかけることによって実現します。「デルタ函数」を避けるためには最初から変数の個数を少なくしておけばよいです。続く
多項分布と多次元正規分布の関係については例のノートに解説を書いておいたのですが、現在停電のせいでサーバー停止中。
p,q,r>0、p+q+r=1とき、それぞれp,q,rの確率で1,2,3の目が出るルーレットをn回まわしたとき、1,2,3の目が出た回数をそれぞれK,L,Mと書きます。K,L,M自身が確率変数。常にK+L+M=nなので、続く
続い、独立な変数は2個。その2個としてK,Lを選びます。K,Lの平均値はそれぞれnp,nqでそれらの分散はそれぞれn(p-p^2),n(q-q^2)になり、それらの共分散は-npqになります。定義と計算はググって下さい。続く
#数楽 だから、X=(K-np)/√n、Y=(L-nq)/√nはどちらも平均0で、それぞれの分散はp-p^2,q-q^2になり、共分散は-pqになります。この計算と中心極限定理を合わせると、nが大きなとき、(X,Y)が〜続く
#数楽 続き〜従う分布はそれらと同じ平均、分散、共分散を持つ2次元正規分布で近似されます。知りたいのはその確率密度函数の具体的な形。対角成分が分散たちで、それ以外の成分が共分散の行列Aを分散共分散行列と呼びます。続く
#数楽 以上の状況で、A={{p-p^2,-pq},{-pq,q-q^2}}なので、A^{-1}=(1/r){{(1-q)/p,1},{1,(1-p)/q}}となる(p=q=r=1/3のとき{{6,3},{3,6}})。

で、一般に分散共分散行列がAで、A^{-1}=[b_{ij}]のとき、対応する平均0の正規分布の確率密度函数はexp(-(1/2)Σ_{i,j} b_{ij} x_i x_j)/√det(2πA)になります。
p=q=r=1/3の場合の確率密度函数のグラフ(定数倍の部分は無視)はすでに投稿したグラフの画像の通りです。http://www.wolframalpha.com/input/?i=z=exp(-(6x**2+6xy+6y**2)/2 …)
リンクがうま行かないので、適当に+を補って下さい。
その方針での計算もStirlingの公式をぶちこんでがんばればできます。でもかなり大変。特性函数の方でn→∞とするのが確率論の教科書によくある方針です。

#数楽 某ノートから多項分布と多次元正規分布とピアソンのカイ二乗統計量の解説部分を抜き出して放流(1/4)多項分布の定義と平均・分散の計算pic.twitter.com/icTBfnO2xD



#数楽 可逆でない分散共分散行列を持つ正規分布も応用上自然に出て来るという事情があるので、多次元正規分布を定義するときに分散共分散行列が可逆という条件を課したくない。そのためのシンプルな方法は特性函数がexp(高々2次函数)になるという条件で定義すること。
#数楽 特性函数を使うということはFourier解析を前提にすること。Fourier解析は普遍的に重要なので使える場合には避けるべきではないと思う。数学の世界では本当にあちこちでFourier変換が出て来る。
#数楽 https://twitter.com/labidochromis/status/769929694393176068 …サイコロを3回ふったとき6の目が出る回数の期待値は0.5で最頻値は0になる。問題:それではサイコロを4回ふったとき、6の目が何回出ることに賭けると当たる確率が一番高いか?期待値は2/3回で0回より1回の方に近い。
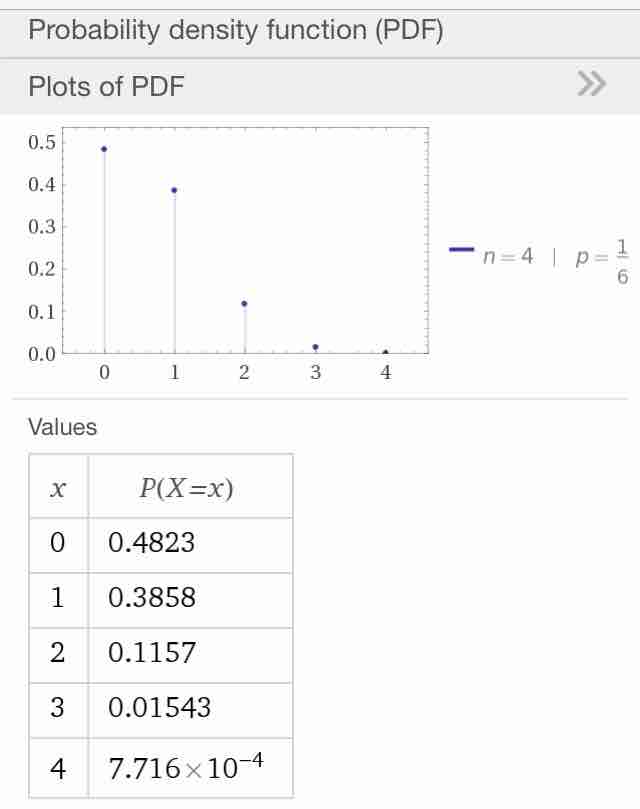
#数楽 1つ前の問題の答は添付画像の通り。添付画像の数値はそれぞれの回数の確率。WolframAlphaを使った→ http://www.wolframalpha.com/input/?i=binomial distribution for p=1/6, n=4 …pic.twitter.com/sIB5G0omcx
5回振ると悩ましいですね。
#数楽 続き。これ「飲み屋での話」なら騙される人が結構いそうだな。「サイコロを4回ふったとき6の目が出る回数の期待値は2/3回だ。0回より1回に近い。だからあなたは1回に賭けたまえ。私は0回に賭けよう。当たるたびに相手から100円もらう。」www
#数楽 iPhoneのWolframAlphaアプリからツイッターにURLをコピー&ペーストするときには、+は全角の+で入力し、^の代わりに**を使うとリンクに失敗しない。汚い方法だが気軽に使える方法。
https://twitter.com/__dalong/status/770014750050836486 …アイコンも含めて非常によくわかっている人のコメントだと感じた。実際に賭博の実験をやってみるとばらつきは結構大きく感じられる。返答連鎖の上の方で400回の賭博の分布を例に出しているが、その400は慎重に選んだ数値。



